学习了一段时间序列,总感觉自己没有完全搞太明白,这里附上一些实验代码,方便后期总结回顾。对于时间序列的预测问题,一般的机器学习算法并没有很占优势,RNN类的算法训练成本又太高,往往不可取,倒是传统的时间序列模型的效果较好,这里对此,进行一定的学习。内容来自互联网
1.定义
顾名思义,时间序列是时间间隔不变的情况下收集的时间点集合。这些集合被分析用来了解长期发展趋势,为了预测未来或者表现分析的其他形式。但是是什么令时间序列与常见的回归问题的不同?
有两个原因:
1、时间序列是跟时间有关的。所以基于线性回归模型的假设:观察结果是独立的,在这种情况下是不成立的。
2、随着上升或者下降的趋势,更多的时间序列出现季节性趋势的形式,如:特定时间框架的具体变化。即:如果你看到羊毛夹克的销售上升,你就一定会在冬季做更多销售。
常用的时间序列模型有AR模型、MA模型、ARMA模型和ARIMA模型等。
1.1 时间序列的预处理
拿到一个观察值序列之后,首先要对它的平稳性和纯随机性进行检验,这两个重要的检验称为序列的预处理。根据检验的结果可以将序列分为不同的类型,对不同类型的序列我们会采用不同的分析方法。
先说下什么是平稳,平稳就是围绕着一个常数上下波动且波动范围有限,即有常数均值 和常数方差。如果有明显的趋势或周期性,那它通常不是平稳序列。序列平稳不平稳,一般采用三种方法检验:
(1)时序图检验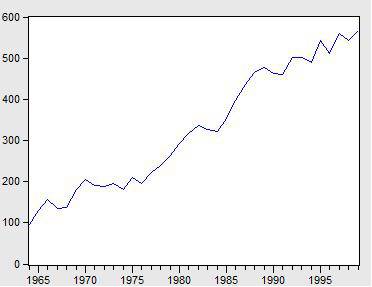
看看上面这个图,很明显的增长趋势,不平稳。
(2)自相关系数和偏相关系数
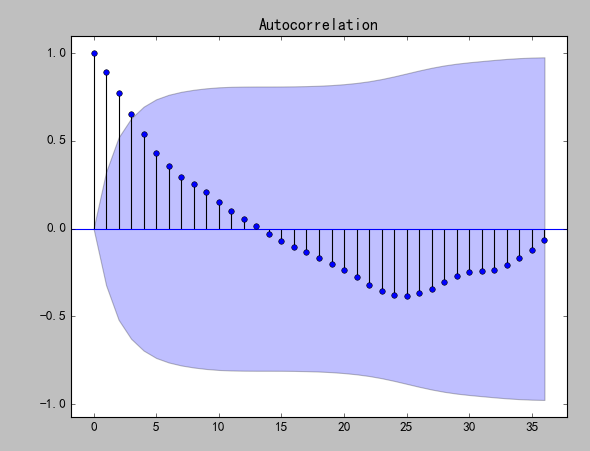
还以上面的序列为例:用SPSS得到自相关和偏相关图。
分析:左边第一个为自相关图(Autocorrelation),第二个偏相关图(Partial Correlation)。
平稳的序列的自相关图和偏相关图要么拖尾,要么是截尾。截尾就是在某阶之后,系数都为 0 ,怎么理解呢,看上面偏相关的图,当阶数为 1 的时候,系数值还是很大,0.914;二阶长的时候突然就变成了 0.050。后面的值都很小,认为是趋于 0 ,这种状况就是截尾。什么是拖尾,拖尾就是有一个缓慢衰减的趋势,但是不都为 0 。
自相关图既不是拖尾也不是截尾。以上的图的自相关是一个三角对称的形式,这种趋势是单调趋势的典型图形,说明这个序列不是平稳序列。
(3)单位根检验
单位根检验是指检验序列中是否存在单位根,如果存在单位根就是非平稳时间序列。
1.2 不平稳,怎么办?
答案是差分,转换为平稳序列。什么是差分?一阶差分指原序列值相距一期的两个序列值之间的减法运算;k阶差分就是相距k期的两个序列值之间相减。如果一个时间序列经过差分运算后具有平稳性,则该序列为差分平稳序列,可以使用ARIMA模型进行分析。
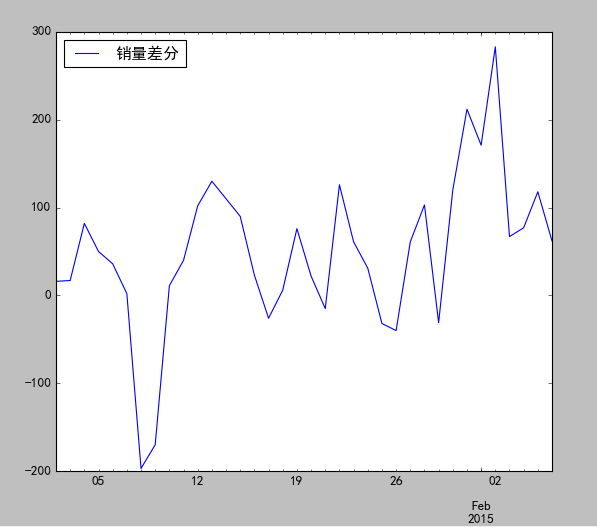
还是上面那个序列,两种方法都证明他是不靠谱的,不平稳的。确定不平稳后,依次进行1阶、2阶、3阶…差分,直到平稳为止。先来个一阶差分,上图:

从图上看,一阶差分的效果不错,看着是平稳的。
平稳性检验过后,下一步是纯随机性检验。
对于纯随机序列,又称白噪声序列,序列的各项数值之间没有任何相关关系,序列在进行完全无序的随机波动,可以终止对该序列的分析。白噪声序列是没有信息可提取的平稳序列。
对于平稳非白噪声序列,它的均值和方差是常数。通常是建立一个线性模型来拟合该序列的发展,借此提取该序列的有用信息。ARMA模型是最常用的平稳序列拟合模型。
1.什么是白噪声?
答:白噪声是指功率谱密度在整个频域内均匀分布的噪声。白噪声或白杂讯,是一种功率频谱密度为常数的随机信号或随机过程。换句话说,此信号在各个频段上的功率是一样的,由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,此信号也因此被称作白噪声。相对的,其他不具有这一性质的噪声信号被称为有色噪声。理想的白噪声具有无限带宽,因而其能量是无限大,这在现实世界是不可能存在的。实际上,我们常常将有限带宽的平整讯号视为白噪音,因为这让我们在数学分析上更加方便。然而,白噪声在数学处理上比较方便,因此它是系统分析的有力工具。一般,只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽,并且在该带宽中其频谱密度基本上可以作为常数来考虑,就可以把它作为白噪声来处理。例如,热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度,通常可以认为它们是白噪声。高斯白噪声:如果一个噪声,它的幅度分布服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。热噪声和散粒噪声是高斯白噪声。所谓高斯白噪声中的高斯是指概率分布是正态函数,而白噪声是指它的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。
高斯白噪声的概念——“白”指功率谱恒定;高斯指幅度取各种值时的概率p (x)是高斯函数
高斯噪声——n维分布都服从高斯分布的噪声
高斯分布——也称正态分布,又称常态分布。对于随机变量X,记为N(μ,σ2),分别为高斯分布的期望和方差。当有确定值时,p (x)也就确定了,特别当μ=0,σ2=1时,X的分布为标准正态分布。2.为什么残差要是白噪声?
答:得到白噪声序列,就说明时间序列中有用的信息已经被提取完毕了,剩下的全是随机扰动,是无法预测和使用的,残差序列如果通过了白噪声检验,则建模就可以终止了,因为没有信息可以继续提取。如果残差不是白噪声,就说明残差中还有有用的信息,需要修改模型或者进一步提取。3.怎样对白噪声进行检验?
答:白噪声检验的步骤为:打开resid序列,view,correlogram,差分阶数选择level,确定,看q统计量的伴随p值是不是很大就行了。
1.3 平稳时间序列建模
某个时间序列经过预处理,被判定为平稳非白噪声序列,就可以进行时间序列建模。
建模步骤:
(1)计算出该序列的自相关系数(ACF)和偏相关系数(PACF);
(2)模型识别,也称模型定阶。根据系数情况从AR(p)模型、MA(q)模型、ARMA(p,q)模型、ARIMA(p,d,q)模型中选择合适模型,其中p为自回归项,d为差分阶数,q为移动平均项数。
下面是平稳序列的模型选择:
| 自相关系数(ACF) | 偏相关系数(PACF) | 选择模型 |
|---|---|---|
| 拖尾 | p阶截尾 | AR(p) |
| q阶截尾 | 拖尾 | MA(q) |
| p阶拖尾 | q阶拖尾 | ARMA(p,q) |
ARIMA 是 ARMA 算法的扩展版,用法类似 。
(3)估计模型中的未知参数的值并对参数进行检验;
(4)模型检验;
(5)模型优化;
(6)模型应用:进行短期预测。
1.4 python实例操作
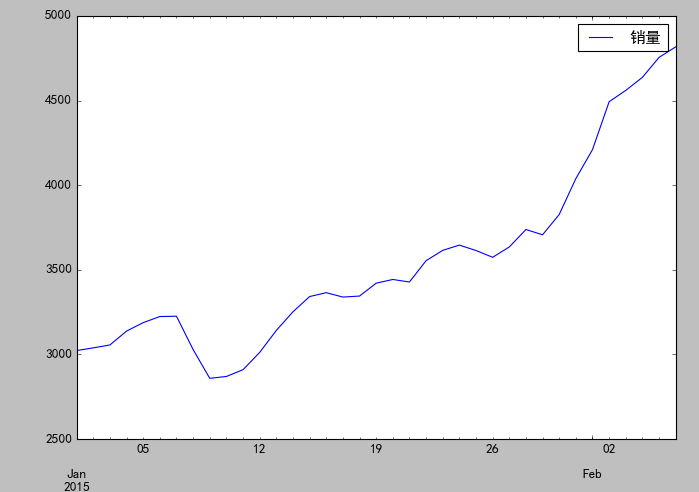
以下为某店铺2015/1/1~2015/2/6的销售数据,以此建模预测2015/2/7~2015/2/11的销售数据。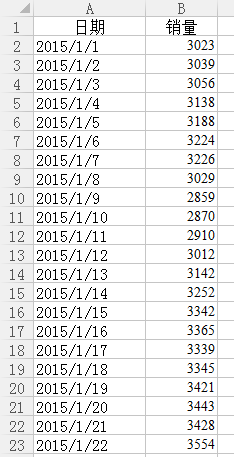
|
|
|
返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

adf值大于三个水平值,p值显著大于0.05,该序列为非平稳序列。
|
|
|
|
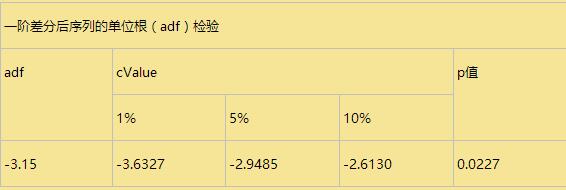
adf值小于两个水平值,p值显著小于0.05,一阶差分后序列为平稳序列。
|
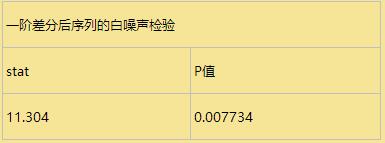
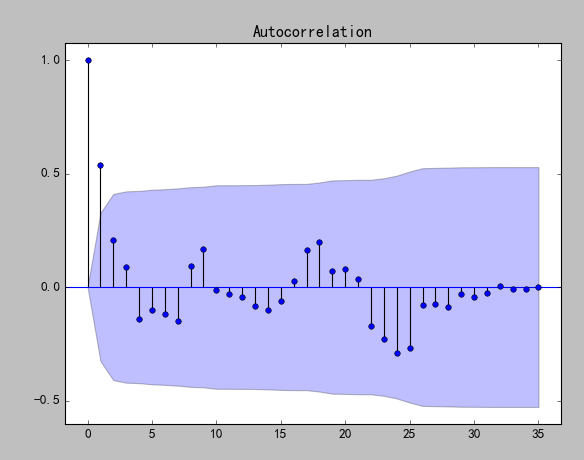
P值小于0.05,所以一阶差分后的序列为平稳非白噪声序列。
|
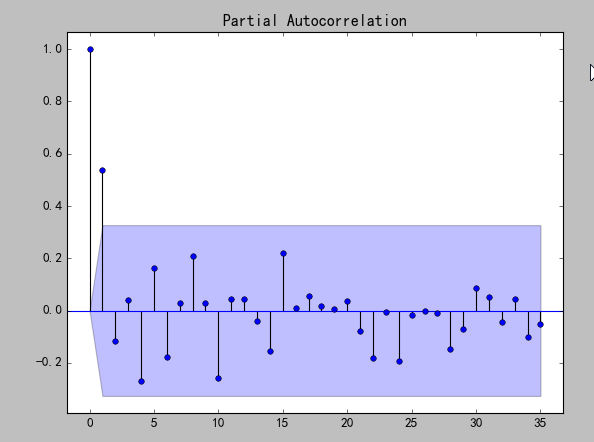
取BIC信息量达到最小的模型阶数,结果p为0,q为1,定阶完成。
|
最终模型预测值如下:
| 2015/2/7 | 2015/2/8 | 2015/2/9 | 2015/2/10 | 2015/2/11 |
|---|---|---|---|---|
| 4874.0 | 4923.9 | 4973.9 | 5023.8 | 5073.8 |
利用模型向前预测的时间越长,预测的误差将会越大,这是时间预测的典型特点。
参数检验如下: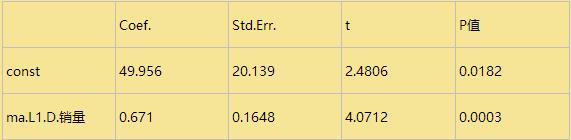
2.TimeSeries
2.1 什么是时间序列
时间序列简单的说就是各时间点上形成的数值序列,时间序列分析就是通过观察历史数据预测未来的值。在这里需要强调一点的是,时间序列分析并不是关于时间的回归,它主要是研究自身的变化规律的(这里不考虑含外生变量的时间序列)。
2.2 为什么用python
用两个字总结“情怀”,爱屋及乌,个人比较喜欢python,就用python撸了。能做时间序列的软件很多,SAS、R、SPSS、Eviews甚至matlab等等,实际工作中应用得比较多的应该还是SAS和R,前者推荐王燕写的《应用时间序列分析》,后者推荐基于R语言的时间序列建模完整教程这篇博文(翻译版)。python作为科学计算的利器,当然也有相关分析的包:statsmodels中tsa模块,当然这个包和SAS、R是比不了,但是python有另一个神器:pandas!pandas在时间序列上的应用,能简化我们很多的工作。
2.3 时间序列分析
2.3.1 基本模型
自回归移动平均模型(ARMA(p,q))是时间序列中最为重要的模型之一,它主要由两部分组成: AR代表p阶自回归过程,MA代表q阶移动平均过程,其公式如下: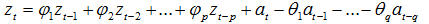
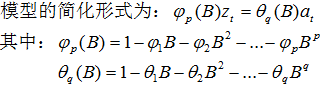
依据模型的形式、特性及自相关和偏自相关函数的特征,总结如下: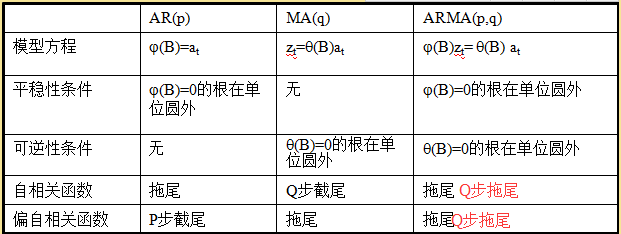
在时间序列中,ARIMA模型是在ARMA模型的基础上多了差分的操作。
2.3.2 pandas时间序列操作
大熊猫真的很可爱,这里简单介绍一下它在时间序列上的可爱之处。和许多时间序列分析一样,本文同样使用航空乘客数据(AirPassengers.csv)作为样例。
数据读取:
|
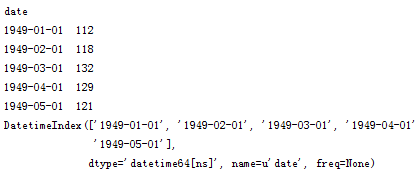
查看某日的值既可以使用字符串作为索引,又可以直接使用时间对象作为索引
|
两者的返回值都是第一个序列值:112
如果要查看某一年的数据,pandas也能非常方便的实现

切片操作:
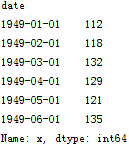
注意时间索引的切片操作起点和尾部都是包含的,这点与数值索引有所不同
pandas还有很多方便的时间序列函数,在后面的实际应用中在进行说明。
2.3.3 平稳性检验
我们知道序列平稳性是进行时间序列分析的前提条件,很多人都会有疑问,为什么要满足平稳性的要求呢?在大数定理和中心定理中要求样本同分布(这里同分布等价于时间序列中的平稳性),而我们的建模过程中有很多都是建立在大数定理和中心极限定理的前提条件下的,如果它不满足,得到的许多结论都是不可靠的。以虚假回归为例,当响应变量和输入变量都平稳时,我们用t统计量检验标准化系数的显著性。而当响应变量和输入变量不平稳时,其标准化系数不在满足t分布,这时再用t检验来进行显著性分析,导致拒绝原假设的概率增加,即容易犯第一类错误,从而得出错误的结论。
平稳时间序列有两种定义:严平稳和宽平稳
严平稳顾名思义,是一种条件非常苛刻的平稳性,它要求序列随着时间的推移,其统计性质保持不变。对于任意的τ,其联合概率密度函数满足: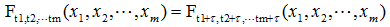
严平稳的条件只是理论上的存在,现实中用得比较多的是宽平稳的条件。
宽平稳也叫弱平稳或者二阶平稳(均值和方差平稳),它应满足:
- 常数均值
- 常数方差
- 常数自协方差
- 平稳性检验:观察法和单位根检验法
基于此,我写了一个名为test_stationarity的统计性检验模块,以便将某些统计检验结果更加直观的展现出来。
从检验结果p值来看,建立的模型效果良好。
|
观察法,通俗的说就是通过观察序列的趋势图与相关图是否随着时间的变化呈现出某种规律。所谓的规律就是时间序列经常提到的周期性因素,现实中遇到得比较多的是线性周期成分,这类周期成分可以采用差分或者移动平均来解决,而对于非线性周期成分的处理相对比较复杂,需要采用某些分解的方法。下图为航空数据的线性图,可以明显的看出它具有年周期成分和长期趋势成分。平稳序列的自相关系数会快速衰减,下面的自相关图并不能体现出该特征,所以我们有理由相信该序列是不平稳的。
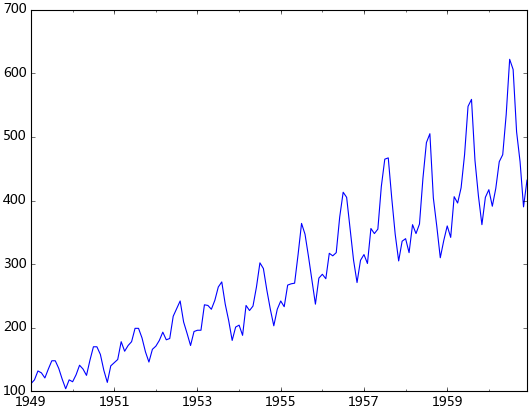

单位根检验:ADF是一种常用的单位根检验方法,他的原假设为序列具有单位根,即非平稳,对于一个平稳的时序数据,就需要在给定的置信水平上显著,拒绝原假设。ADF只是单位根检验的方法之一,如果想采用其他检验方法,可以安装第三方包arch,里面提供了更加全面的单位根检验方法,个人还是比较钟情ADF检验。以下为检验结果,其p值大于0.99,说明并不能拒绝原假设。
2.3.4 平稳性处理
由前面的分析可知,该序列是不平稳的,然而平稳性是时间序列分析的前提条件,故我们需要对不平稳的序列进行处理将其转换成平稳的序列。
a. 对数变换
对数变换主要是为了减小数据的振动幅度,使其线性规律更加明显(我是这么理解的时间序列模型大部分都是线性的,为了尽量降低非线性的因素,需要对其进行预处理,也许我理解的不对)。对数变换相当于增加了一个惩罚机制,数据越大其惩罚越大,数据越小惩罚越小。这里强调一下,变换的序列需要满足大于0,小于0的数据不存在对数变换。
|
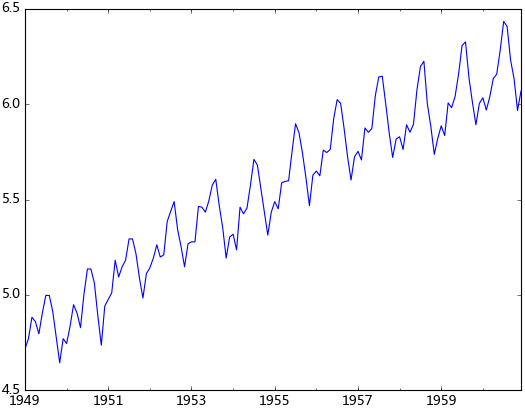
b. 平滑法
根据平滑技术的不同,平滑法具体分为移动平均法和指数平均法。
移动平均即利用一定时间间隔内的平均值作为某一期的估计值,而指数平均则是用变权的方法来计算均值
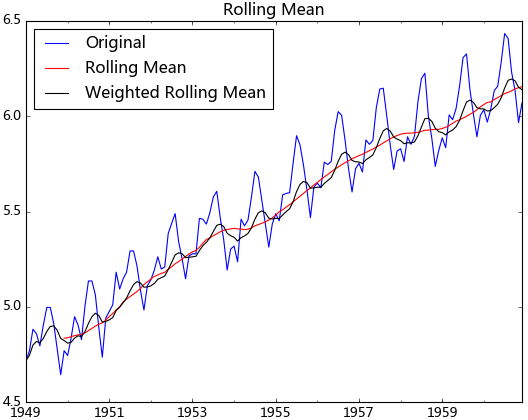
从上图可以发现窗口为12的移动平均能较好的剔除年周期性因素,而指数平均法是对周期内的数据进行了加权,能在一定程度上减小年周期因素,但并不能完全剔除,如要完全剔除可以进一步进行差分操作。
c. 差分
时间序列最常用来剔除周期性因素的方法当属差分了,它主要是对等周期间隔的数据进行线性求减。前面我们说过,ARIMA模型相对ARMA模型,仅多了差分操作,ARIMA模型几乎是所有时间序列软件都支持的,差分的实现与还原都非常方便。而statsmodel中,对差分的支持不是很好,它不支持高阶和多阶差分,为什么不支持,这里引用作者的说法:

作者大概的意思是说预测方法中并没有解决高于2阶的差分,有没有感觉很牵强,不过没关系,我们有pandas。我们可以先用pandas将序列差分好,然后在对差分好的序列进行ARIMA拟合,只不过这样后面会多了一步人工还原的工作。
|

从上面的统计检验结果可以看出,经过12阶差分和1阶差分后,该序列满足平稳性的要求了。
d. 分解
所谓分解就是将时序数据分离成不同的成分。statsmodels使用的X-11分解过程,它主要将时序数据分离*成长期趋势、季节趋势和随机成分。与其它统计软件一样,statsmodels也支持两类分解模型,加法模型和乘法模型,这里我只实现加法,乘法只需将model的参数设置为”multiplicative”即可。
|
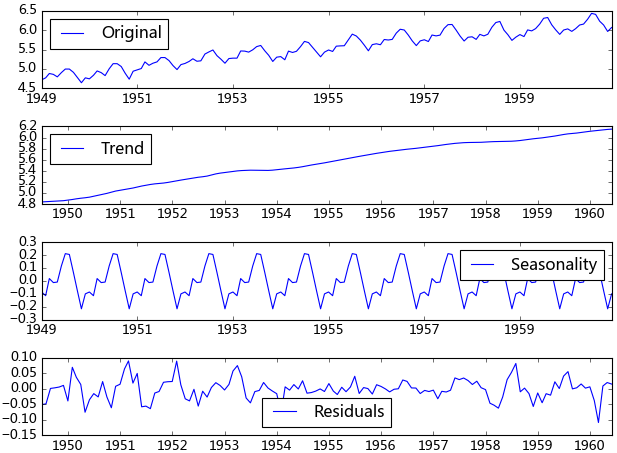
得到不同的分解成分后,就可以使用时间序列模型对各个成分进行拟合,当然也可以选择其他预测方法。我曾经用过小波对时序数据进行过分解,然后分别采用时间序列拟合,效果还不错。由于我对小波的理解不是很好,只能简单的调用接口,如果有谁对小波、傅里叶、卡尔曼理解得比较透,可以将时序数据进行更加准确的分解,由于分解后的时序数据避免了他们在建模时的交叉影响,所以我相信它将有助于预测准确性的提高。
2.3.5 模型识别
在前面的分析可知,该序列具有明显的年周期与长期成分。对于年周期成分我们使用窗口为12的移动平进行处理,对于长期趋势成分我们采用1阶差分来进行处理。
|

观察其统计量发现该序列在置信水平为95%的区间下并不显著,我们对其进行再次一阶差分。再次差分后的序列其自相关具有快速衰减的特点,t统计量在99%的置信水平下是显著的,这里我不再做详细说明。
|
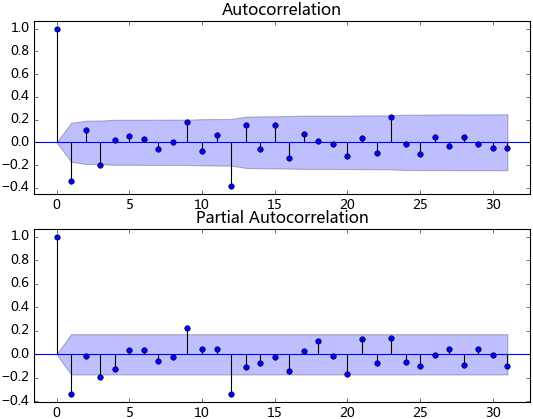
数据平稳后,需要对模型定阶,即确定p、q的阶数。观察上图,发现自相关和偏相系数都存在拖尾的特点,并且他们都具有明显的一阶相关性,所以我们设定p=1,q=1。下面就可以使用ARMA模型进行数据拟合了。这里我不使用ARIMA(ts_diff_1, order=(1, 1, 1))进行拟合,是因为含有差分操作时,预测结果还原老出问题,至今还没弄明白。
|
2.3.6 样本拟合
模型拟合完后,我们就可以对其进行预测了。由于ARMA拟合的是经过相关预处理后的数据,故其预测值需要通过相关逆变换进行还原。
|
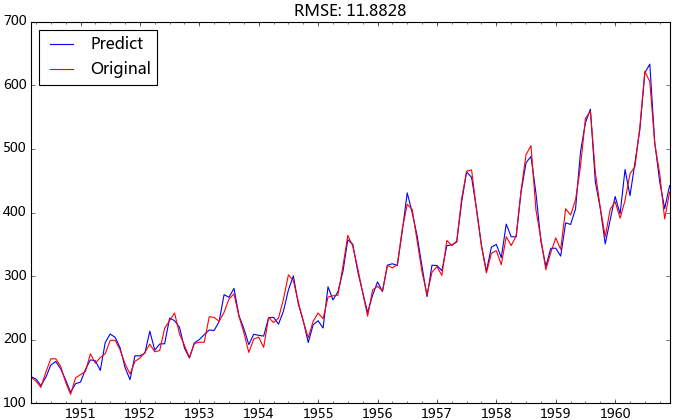
我们使用均方根误差(RMSE)来评估模型样本内拟合的好坏。利用该准则进行判别时,需要剔除“非预测”数据的影响。
|

观察上图的拟合效果,均方根误差为11.8828,感觉还过得去。
2.3.7 完善ARIMA模型
前面提到statsmodels里面的ARIMA模块不支持高阶差分,我们的做法是将差分分离出来,但是这样会多了一步人工还原的操作。基于上述问题,我将差分过程进行了封装,使序列能按照指定的差分列表依次进行差分,并相应的构造了一个还原的方法,实现差分序列的自动还原。
|
现在我们直接使用差分的方法进行数据处理,并以同样的过程进行数据预测与还原。
|
是不是发现这里的预测结果和上一篇的使用12阶移动平均的预测结果一模一样。这是因为12阶移动平均加上一阶差分与直接12阶差分是等价的关系,后者是前者数值的12倍,这个应该不难推导。
对于个数不多的时序数据,我们可以通过观察自相关图和偏相关图来进行模型识别,倘若我们要分析的时序数据量较多,例如要预测每只股票的走势,我们就不可能逐个去调参了。这时我们可以依据BIC准则识别模型的p,q值,通常认为BIC值越小的模型相对更优。这里我简单介绍一下BIC准则,它综合考虑了残差大小和自变量的个数,残差越小BIC值越小,自变量个数越多BIC值越大。个人觉得BIC准则就是对模型过拟合设定了一个标准(过拟合这东西应该以辩证的眼光看待)。
|
相对最优参数识别结果:BIC: -1090.44209358 p: 0 q: 1 , RMSE:11.8817198331。我们发现模型自动识别的参数要比我手动选取的参数更优。
2.3.8 滚动预测
所谓滚动预测是指通过添加最新的数据预测第二天的值。对于一个稳定的预测模型,不需要每天都去拟合,我们可以给他设定一个阀值,例如每周拟合一次,该期间只需通过添加最新的数据实现滚动预测即可。基于此我编写了一个名为arima_model的类,主要包含模型自动识别方法,滚动预测的功能,详细代码可以查看附录。数据的动态添加:
|
现在我们就可以使用滚动预测的方法向外预测了,取1957年之前的数据作为训练数据,其后的数据作为测试,并设定模型每第七天就会重新拟合一次。这里的diffed_ts对象会随着add_today_data方法自动添加数据,这是由于它与add_today_data方法中的d_ts指向的同一对象,该对象会动态的添加数据。
|
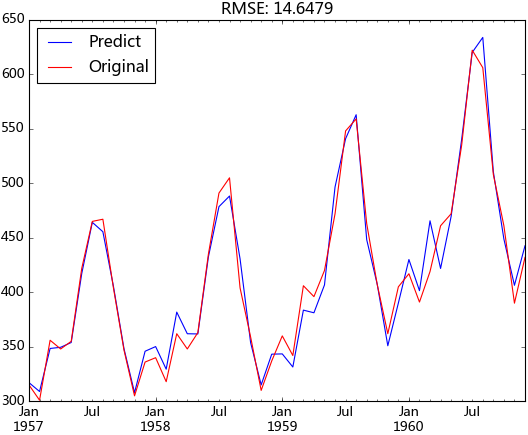
动态预测的均方根误差为:14.6479,与前面样本内拟合的均方根误差相差不大,说明模型并没有过拟合,并且整体预测效果都较好。
2.3.9 模型序列化
在进行动态预测时,我们不希望将整个模型一直在内存中运行,而是希望有新的数据到来时才启动该模型。这时我们就应该把整个模型从内存导出到硬盘中,而序列化正好能满足该要求。序列化最常用的就是使用json模块了,但是它是时间对象支持得不是很好,有人对json模块进行了拓展以使得支持时间对象,这里我们不采用该方法,我们使用pickle模块,它和json的接口基本相同,有兴趣的可以去查看一下。我在实际应用中是采用的面向对象的编程,它的序列化主要是将类的属性序列化即可,而在面向过程的编程中,模型序列化需要将需要序列化的对象公有化,这样会使得对前面函数的参数改动较大,我不在详细阐述该过程。
总结
与其它统计语言相比,python在统计分析这块还显得不那么“专业”。随着numpy、pandas、scipy、sklearn、gensim、statsmodels等包的推动,我相信也祝愿python在数据分析这块越来越好。与SAS和R相比,python的时间序列模块还不是很成熟,我这里仅起到抛砖引玉的作用,希望各位能人志士能贡献自己的力量,使其更加完善。实际应用中我全是面向过程来编写的,为了阐述方便,我用面向过程重新罗列了一遍,实在感觉很不方便。原本打算分三篇来写的,还有一部分实际应用的部分,不打算再写了,还请大家原谅。实际应用主要是具体问题具体分析,这当中第一步就是要查询问题,这步花的时间往往会比较多,然后再是解决问题。以我前面项目遇到的问题为例,当时遇到了以下几个典型的问题:1.周期长度不恒定的周期成分,例如每月的1号具有周期性,但每月1号与1号之间的时间间隔是不相等的;2.含有缺失值以及含有记录为0的情况无法进行对数变换;3.节假日的影响等等。
代码:
|
3.LSTM
关于技术理论部分,可以参考这两篇文章(RNN、LSTM),本文主要从数据、代码角度,利用LSTM进行时间序列预测。
时间序列(或称动态数列)是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列。时间序列分析的主要目的是根据已有的历史数据对未来进行预测。
时间序列构成要素:长期趋势,季节变动,循环变动,不规则变动
长期趋势( T )现象在较长时期内受某种根本性因素作用而形成的总的变动趋势
季节变动( S )现象在一年内随着季节的变化而发生的有规律的周期性变动
循环变动( C )现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动
不规则变动(I )是一种无规律可循的变动,包括严格的随机变动和不规则的突发性影响很大的变动两种类型
(1)原始时间序列数据(只列出了18行)
1455.219971
1399.420044
1402.109985
1403.449951
1441.469971
1457.599976
1438.560059
1432.25
1449.680054
1465.150024
1455.140015
1455.900024
1445.569946
1441.359985
1401.530029
1410.030029
1404.089966
1398.560059
(2)处理数据使之符合LSTM的要求
为了更加直观的了解数据格式,代码中加入了一些打印(print),并且后面加了注释,就是输出值
|
(3)LSTM模型
本文使用的是keras深度学习框架,读者可能用的是其他的,诸如theano、tensorflow等,大同小异。
LSTM的结构可以自己定制,Stack LSTM or Bidirectional LSTM
|
(4)LSTM训练预测
1.直接预测
|
2.滚动预测
|
3.滑动窗口+滚动预测
|
完整代码:
|
QUESTION:
1.到现在也搞不懂是什么时候检测白噪声序列,是检测差分后的时间序列,还是差分后的残差。网上文档不一啊,坑人mmd。
2.ARMA(ts, (p, q))中的ts是原时间序列,还是经过差分后的时间序列,为啥网上一些博客,有的时候是原时间序列,有的时候是经过差分后的时间序列。
3.ARIMA(ts, (p,d,q)选择p,q时,老是会报错。写个循环把,又tam的特别慢
4.R语言里面mmd的就有一个auto.arima()自动获取ARIMA模型,妈的为啥python没有,cao
5.网上的一些狗屁教程标题上写的时ARIMA,实际上里面先作一系列差分操作,然后又用ARMA模型判断选择p、q,你妹妹的。丫的,自己傻傻分不清还教别人
SUMMARY
1.首先,拿到数据先把它转换为timeseries
2.判断是否平稳,画个图先预判一下,实际操作可以用adf值(python中用这个函数sm.tsa.stattools.adfuller(ts))
看
Test Statistic Value是不是要小于这3个Critical Value(1%)、Critical Value(5%)、Critical Value(10%)对应的值
p-value小于0.05
3.不平稳的话可以进行(对数log、差分diff等)
4.差分后再重复步骤2,一般来说差分一次就基本平稳了,然后就是选择p、q参数了,网上又好多代码自动选择,到时如果迭代次数过多的话,卡死你。要想快速人工进行筛选的话,可以用2个函数acf()和pcf()画个图,自己看一下,进行个初步筛选q值和p值。
5.白噪声检验((说白了白噪声就是不相关的随机变量序列,怎么理解呢?)[https://zhuanlan.zhihu.com/p/26227700])就是Ljung-Box 指标。这个指标可对每一个时间序列的延迟进行显著性的评估。判定技巧是,P-value点的高度越高,随机的可能性越大,我们的模型越可信。所谓自相关是当期值和往期值有线性关系,一般时间序列建模要求残差是独立同分布的白噪声序列,如果残差存在自相关也说明变量的信息没被模型挖空。
来源:
相关博客:
(ARIMA模型文档)[http://www.statsmodels.org/stable/generated/statsmodels.tsa.arima_model.ARIMA.html]
(用ARIMA模型做需求预测)[https://www.jianshu.com/p/f547bb4b50c3?utm_campaign=maleskine&utm_content=note&utm_medium=seo_notes&utm_source=recommendation]
http://www.cnblogs.com/foley/p/5582358.html
http://www.10tiao.com/html/284/201608/2652390079/1.html
http://blog.csdn.net/a819825294/article/details/54376781
http://www.cnblogs.com/arkenstone/p/5794063.html

